Uncovering Market Sentiment: The Commitment of Traders Report

In the ever-evolving world of financial markets, understanding the forces behind price movements can feel like chasing the wind. But what if you had a window into the intentions of the market's most influential players? This is where the Commitment of Traders (COT) Report comes into play—a treasure trove of data that offers a rare glimpse into the positions taken by the giants of the financial and commodity markets. To understand its importance, let’s explore its origins, evolution, and practical applications.

A Historical Backdrop: The Birth of the COT Report

The story of the COT Report begins in the early 20th century, a period when commodity trading started to take on a greater role in supporting global supply chains. Farmers, merchants, and industrial producers used the futures markets to hedge their risks, creating the need for transparency in these contracts. In 1924, the U.S. Department of Agriculture began releasing basic market data, laying the groundwork for what would eventually become the COT Report.

However, it wasn't until the formation of the Commodity Futures Trading Commission (CFTC) in 1974 that the report as we know it began to take shape. The CFTC, established to regulate the futures and options markets, aimed to provide greater transparency to help traders make informed decisions and to ensure a fair marketplace. By 1982, the COT Report was released regularly, offering an unparalleled look at how major market players were positioning themselves across different asset classes—from grains and livestock to precious metals and financial futures.

Breaking Down the COT Report: Who's Who?

The COT Report, published every Friday by the CFTC, is a detailed summary of the positions held by different market participants as of the previous Tuesday. Traders are categorized into three main groups:

• Commercial Traders (Hedgers): These are the producers and users of commodities—such as farmers, oil companies, and airlines—who use futures contracts to protect themselves against price volatility. Their goal is to minimize risk rather than speculate on price changes.
• Non-Commercial Traders (Speculators): These are the hedge funds, financial institutions, and professional investors looking to profit from price movements. They add liquidity to the markets and often take on risks that hedgers wish to avoid.
• Non-Reportable Traders: This group includes smaller traders whose positions are below the reporting threshold. Their activities are often considered less impactful, but they still contribute to overall market dynamics.

The COT Report reveals each group’s long (betting on price increases), short (betting on price decreases), and spreading (holding both long and short positions) activities. It’s an indispensable tool for traders who wish to understand the psychology and intentions of market participants.

The Commodity Index Traders (CIT) Supplement

In addition to the COT Report, the Commodity Index Traders (CIT) Report offers further insights into market dynamics, particularly regarding the activity of index funds. The CIT Report was introduced in 2007 in response to growing interest in the role of commodity index investments, which had become an increasingly popular way for investors to gain exposure to commodities as an asset class.

The CIT Report provides information on the positions held by index traders, who are typically institutions managing large sums of money and tracking commodity indexes. These traders often hold long positions to gain exposure to commodity price movements, rather than speculating on short-term price changes. The inclusion of CIT data allows traders to better understand the impact of passive investment flows on commodity markets.

The CIT Report can be particularly useful for:

• Understanding Investment Flows: By analyzing index trader positions, market participants can get a sense of how much capital is flowing into or out of commodities through index funds, which can significantly impact prices.
• Complementing COT Analysis: The CIT data, when used alongside the COT Report, provides a more comprehensive picture of market sentiment, especially in markets heavily influenced by passive investment strategies.

How Traders Use the COT Report: From Strategy to Insight

The COT Report has become a cornerstone of market analysis for many traders, especially those seeking to understand the sentiment and positioning in key markets. Here’s how it is commonly used:

1. Gauging Market Sentiment

The COT Report serves as a barometer of market sentiment. By examining the net positions of non-commercial traders, one can gauge whether there is a strong bullish or bearish sentiment in the market. If speculators are heavily long on crude oil, for instance, it may indicate optimism about rising energy prices.

2. Identifying Potential Reversals

Some traders use the COT Report as a contrarian indicator. When speculative traders hold extreme positions—either long or short—it can signal that the market is overextended and due for a correction. For example, if speculators are overwhelmingly short on a commodity, it could imply that selling pressure may be exhausted, increasing the likelihood of a reversal to the upside.

3. Confirming Trends

For trend-following traders, the COT Report is an excellent tool to confirm existing trends. If both commercial and non-commercial traders are aligned in a particular direction, it often indicates a strong underlying trend. By aligning their positions with the sentiment revealed in the report, traders can add an additional layer of confidence to their strategies.

The COT Report in Action: A Practical Example

Consider an example involving the gold market. Suppose the latest COT Report shows a substantial increase in long positions by commercial traders, paired with a reduction in short positions by non-commercial traders. This could be interpreted as a sign that major players expect gold prices to rise, possibly due to economic uncertainty or a weakening dollar. A trader observing this trend might decide to take a long position, anticipating a continuation of the bullish sentiment.

On the other hand, if speculative traders hold an unusually large number of long positions, a contrarian trader might see this as a potential peak in optimism—a signal that the market could be vulnerable to a pullback.

Challenges and Limitations

Despite its usefulness, the COT Report does come with certain limitations. The data is released with a three-day lag, meaning that the market might have moved significantly between the report's compilation and its release. Additionally, while the COT Report shows net positions, it doesn't reveal the motivations behind these positions, which could vary widely depending on broader market conditions or individual strategies.

Furthermore, the interpretation of COT data requires experience. Identifying extremes is not always straightforward, and what constitutes an "extreme" position can vary across different markets and periods.

A Window into Market Dynamics

The Commitment of Traders Report is far more than just a list of numbers—it’s a narrative of market psychology, sentiment, and positioning. By offering insights into the activities of major players, it allows traders to make more informed decisions, whether they are hedging against risks or seeking profitable opportunities. As with all tools, the key to using the COT effectively lies in understanding its nuances, combining it with other forms of analysis, and recognizing its limitations.

Whether you’re a commodity trader seeking an edge or a financial enthusiast aiming to understand market sentiment, the COT Report is a powerful resource—one that continues to help traders navigate the intricate dance of the financial markets.

Understanding the Role of Normal Distribution in Mathematical Finance

In the world of mathematical finance, the normal distribution is one of the foundational building blocks used to model financial variables and make sense of market behavior. Whether you’re pricing options, evaluating risk, or building predictive models, understanding the normal distribution can give you powerful insights into the financial landscape. Let's explore how the normal distribution is applied in finance and why it is so important.

What Is Normal Distribution?

The normal distribution, often referred to as the bell curve due to its characteristic shape, is a probability distribution that describes how values of a random variable are likely to be distributed. It is symmetric around its mean, with most of the data points clustering around the center, and fewer points occurring as we move away from the mean.

In finance, we often use normal distribution to model asset returns, because it is mathematically convenient and aligns well with historical data for many financial metrics over short periods. The distribution is characterized by two parameters: the mean (which represents the average return) and the standard deviation (which indicates the degree of variation or volatility).

Mathematical Proof of Normal Distribution Properties

To understand the role of normal distribution in finance, it is essential to grasp some of its mathematical properties.

The probability density function (PDF) of a normal distribution is given by:

    f(x) = (1 / (σ√2π)) * e^(-(x - μ)^2 / 2σ^2)
    

Where:

• μ is the mean of the distribution.
• σ is the standard deviation.
• x is the random variable.

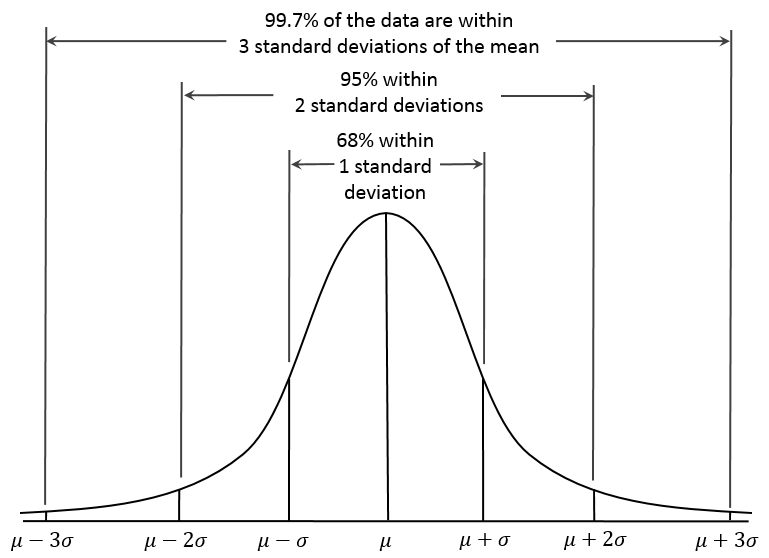
The PDF represents the likelihood of different outcomes and is characterized by the symmetric bell curve shape, with the peak at the mean μ. The area under the curve represents the total probability, which equals 1.

For example, using the empirical rule (or 68-95-99.7 rule), we know that for a normal distribution:

• Approximately 68% of the data lies within one standard deviation of the mean.
• About 95% lies within two standard deviations.
• Roughly 99.7% lies within three standard deviations.

Applications in Mathematical Finance

1. Modeling Asset Returns

Financial analysts commonly assume that returns on assets, such as stocks or portfolios, follow a normal distribution, especially over short time horizons. This assumption allows for easier calculations of probabilities related to returns and risk. For example, by assuming normal distribution, we can estimate the probability that a given stock’s return will fall within a certain range over a period of time.

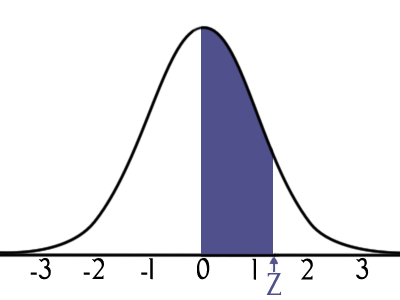
Example: Suppose the daily return of a stock is normally distributed with a mean of 0.1% and a standard deviation of 1%. We can calculate the probability that the return will fall between -1.9% and 2.1% by using the properties of the normal distribution, which gives us about a 95% confidence interval.

2. Calculating Value at Risk (VaR)

Value at Risk (VaR) is a risk management tool that quantifies the maximum expected loss over a specified time period at a given confidence level. The normal distribution plays a crucial role here, as it allows us to compute the likelihood of extreme losses by focusing on the distribution’s tail. Using the properties of the normal distribution, financial institutions can estimate potential losses and establish risk management strategies.

Mathematical Example: If the returns of a portfolio are normally distributed with a mean of 0.5% and a standard deviation of 2%, we can calculate the VaR at a 95% confidence level. Using the inverse of the cumulative distribution function (CDF), we find that the VaR is approximately -2.78%, indicating that there is a 5% chance that the portfolio will lose more than 2.78% in a given period.

3. Black-Scholes Option Pricing Model

The Black-Scholes model, one of the most widely used tools for pricing options, relies on the assumption that the returns of the underlying asset follow a normal distribution. The model uses the concept of log-normality (which is closely related to normal distribution) to estimate the price of options. This is based on the idea that while asset prices cannot go below zero, their returns can still be symmetrically distributed around a mean.

Example: Suppose an investor wants to price a call option for a stock currently trading at $50, with a volatility (standard deviation) of 20%, a risk-free rate of 5%, and a time to maturity of 1 year. Using the Black-Scholes formula, which incorporates the assumption of normally distributed returns, the model will provide an estimate of the fair price of the option.

4. Portfolio Optimization

Harry Markowitz's Modern Portfolio Theory (MPT) also hinges on the assumption of normally distributed returns. Investors use the concept of normal distribution to model and quantify the risk and expected return of different asset combinations. By understanding how these returns are distributed, it becomes possible to build efficient portfolios that maximize return for a given level of risk.

Real-Life Example: Suppose an investor is deciding how to allocate capital between two assets, A and B. By assuming that the returns are normally distributed, the investor can use MPT to find the optimal weights that minimize risk while achieving a target return. The covariance between the assets, combined with their means and standard deviations, helps determine the efficient frontier, guiding the investor’s decision-making process.

Limitations of Using Normal Distribution

While the normal distribution is powerful, it's not without limitations. Real financial returns often exhibit fat tails and skewness, meaning that extreme events (like market crashes) happen more frequently than what would be predicted by a perfect normal distribution. This phenomenon is why some models, like the Black-Scholes, may underestimate the probability of large market moves.

Additionally, the assumption of normal distribution does not account for market behavior driven by emotions or external shocks, which can lead to more erratic price movements. Thus, although the normal distribution is a useful starting point, analysts often use more advanced models, such as those incorporating leptokurtic or heavy-tailed distributions, to capture these nuances.

Conclusion

The normal distribution is a cornerstone of mathematical finance, enabling analysts to model returns, measure risk, and optimize portfolios with relative ease. Its convenient mathematical properties make it an essential tool, particularly in the areas of option pricing, risk management, and investment strategy. However, it’s crucial for practitioners to be mindful of its limitations and consider supplementary models when dealing with real-world financial data.

By appreciating both the strengths and weaknesses of the normal distribution, you can develop a more nuanced understanding of financial markets and make better-informed decisions in a complex environment.